Acids & Bases Problem Set

Acids & Bases Problem Set

Question 10: Relationship between pK_a and pH

Tutorial to help answer the question

The correct operational relationship between pK_a and pH is that:

A. both are log functions.

B. both are always < 7 for acids, and >7 for bases.

C. These two concepts are not operationally related in any way since biological fluids contains mixtures of too many acids and bases.

D. When pH = pK_a , the compound in question will have a charge of +0.5.

E. When pH = pK_a , the ionizable compound in question (whether acid or base) will be half protonated and half deprotonated.

Tutorial

pKa and pH

The "operational" relationship between pKa and pH is mathematically represented by Henderson-Hasselbach equation:

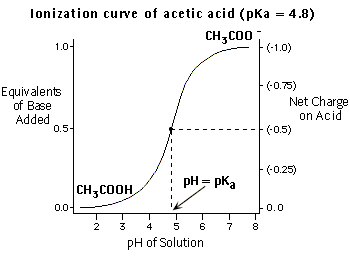
pH = pK_a + log [A^-] / [HA]

where [A^-] represents the deprotonated form and [HA] represents the protonated form.

One oft-cited solution to this equation is obtained by arbitrarily setting pH = pKa.

In this case, log([A^-] / [HA]) = 0, and [A^-] / [HA] = 1.

In words, this means that when the pH is equal to the pK_a of the acid, there are equal amounts of protonated and deprotonated acid molecules. This same relationship holds for bases as well, with [B] substituting for [A^-] as the deprotonated form, and [HB⁺] substituting for [HA] as the protonated form. It should be emphasized that the Henderson-Hasselbach relationship holds for a specified acid or base even if multiple acids or bases are present.

Other solutions to the Henderson-Hasselbach equation over a range of pH values are displayed in the following figure (for acetic acid).

"Net charge on acid" refers to the average of all acid molecules in the solution.

Several points about this graph deserve mention:

At the pK_a , the acid is 50% deprotonated.
At the 1 pH unit above (below) the pK_a , the acid is 90% deprotonated (protonated).
At 2 pH unit above (below) the pK_a , the acid is 99% deprotonated (protonated).
At 3 pH unit above (below) the pK_a , the acid is 99.9% deprotonated (protonated).
When fully protonated, charge on acetic acid is 0.
When fully deprotonated, charge on acetate is -1.

The Biology Project
Department of Biochemistry and Molecular Biophysics
The University of Arizona
January 6, 1999
Revised: October 2004
Contact the Development Team